物理与材料科学学院学生工作一直以增长学生才干和培养学生创新精神为宗旨,培育学术氛围。学院特别重视本科生科研兴趣培养,着力通过科研项目、竞赛、沙龙等方式挖掘本科生科研能力潜质,也形成了一个比较成熟的体系。同时以学院“菁英班”建设为示范,倡导优良学风。本科科研氛围的营造下,取得了一定的成效,在刚刚过去的2018年里,我院本科生发表高水平学术论文2篇。
其中,2014级本科生王绍君以第一作者在Phys. Rev. D 97, 024039 (2018)(SCI一区期刊)发表题为“Maximal volume behind horizons without curvature singularity”的学术论文。
黑洞的概念早已在1916年被提出,但是黑洞体积的计算一直以来是一个多家争鸣,悬而未决的问题。而今,结合量子引力理论,这个问题已经有多种解决方案。其中,一个经典范例是Stanford和Susskind所提出的复杂性-体积对偶猜想。2015年,Christodoulou和Rovelli提出,将黑洞的体积定义为由事件视界限定的最大类空超表面的大小[Phys. Rev. D 91, 064046 (2015)]。迄今为止的计算工作中,理论物理学家主要关注具有曲率奇点的黑洞内部体积的计算。对于正则黑洞内部以及de Sitter事件视界外的区域,它们是有事件视界却无曲率奇点的。然而,在无限远的空间处,时空是渐近平直的,这对黑洞视界内部的求解带来了复杂性。
我院王焘副教授以及本科生王绍君、郭新旋针对以上的问题进行分析研究。首次定义了复杂性是在AdS边界上的一个状态,为了应用复杂性-体积对偶的观点,作者在渐近AdS时空中进行研究。受到Fan的启发,作者创新出一种在一类爱因斯坦引力解中进行宇宙学常数转换的计算方法,应用于解决上述时空的问题,并且应用Christodoulou和Rovelli对黑洞体积的定义,以及Stanford和Ssuskind的复杂-体积对偶猜想,来获得这种渐近AdS解。
作者分别在渐近平直时空和AdS时空中,数值计算了无曲率奇异的规则黑洞的最大体积,数值计算了AdS正则黑洞中复杂性-体积对偶,数值计算并得到了de Sitter事件视界外最大体积的解析表达式。
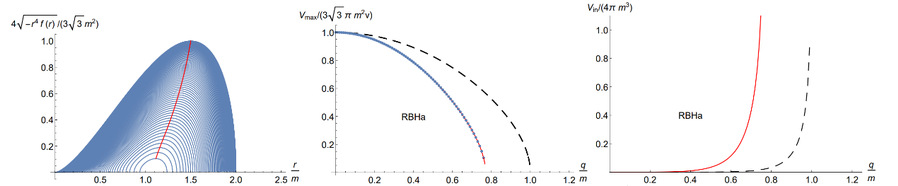
图1
左、中图:最大体积的增长率(已Schwarzschild归一化)和较大v的关系。
右图:内视界内的体积(已4πm3归一化)和q/m增长的关系。黑线为RN黑洞情况作为对比。
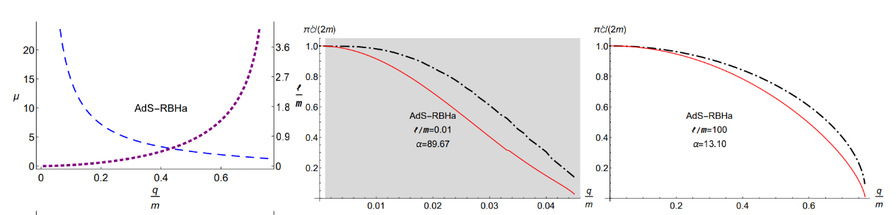
图2
左图:化学式μ以及AdS半径l/m关于q/m的曲线。
中、右图:AdS半径l为m/100和100m时复杂性增长率及其边界。阴影部分,基态是极端黑洞;白色部分基态为真空。
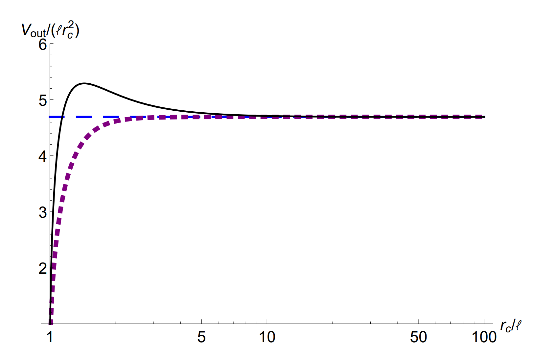
图3 de-Sitter视界外的体积。
黑色实线、紫色虚线和蓝色虚线分别表示解析方程的第一行、第三行和最后一行的数值结果。
作者提出的边界标度是特别的,它依赖于Schwarzschild-AdS黑洞的复杂性增长极限是饱和的假设,可为理论物理工作者提供将其在RN-AdS和Kerr-AdS黑洞以及其他几何结构计算的新思路。
2015级本科生潘晟哲也以第一作者在美国光学学会OSA Continuum杂志上发表了题为“Measuring orbital angular momentums of light based on petal interference patterns”的论文。论文指导老师为我院尹亚玲副教授。
光学涡旋由于具有轨道角动量,在光通信、粒子操控、图像处理和量子信息等领域引起了广泛关注。在这些应用中,光学涡旋所含轨道角动量的测量和验证在相关研究中具有重要意义。近年来,测量光束的轨道角动量的方法主要有干涉法、小孔衍射法和柱透镜法等,其中报道的很多干涉法都采用了Mach-Zehnder干涉仪的方案,用分束器将一束光分成两束之后进行合束再干涉,但是在这些实验中并没有控制干涉光路的位相,所以并不是真正的干涉,而是两路光强度的叠加,或者是不同偏振模式的叠加。潘晟哲提出了一种更为简单的干涉法,主要利用了空间光调制器对光束不完全调制的特性,有一部分的未调制光和调制光叠加在一起,这两束光的位相差恒定,产生螺旋花瓣状的干涉图样。由于实验和模拟结果的完全符合,可以得到干涉图样的光强分布和相位分布,不管是干涉图样中花瓣的个数,还是相位分布中的角向周期数,都对应了光束携带的轨道角动量的值。因此达到了仅用一束光测量光束的轨道角动量的目的。
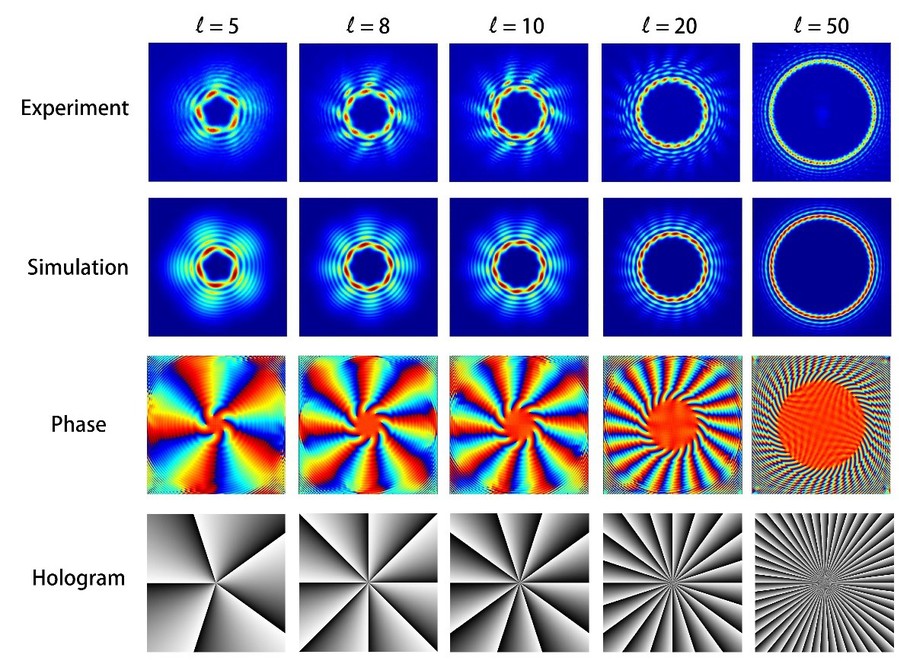
图4 不同阶轨道角动量光束得到的干涉图样的光强分布和相位分布以及对应的全息图
在新的一年里,学院将继续鼓励学生课外学术科技竞赛、本科生科研项目训练、物理专业类竞赛、学术讲座等科技活动启发学生科研灵感,再接再厉,取得更多更高水平的学术成果。